Specifying models with demes
New in version 1.1, moments can compute the SFS and LD statistics
directly from a demes-formatted demographic model. To learn about how to
describe a demographic model using demes, head to the demes repository or documentation to learn
about specifying multi-population demographic models using demes.
What is demes?
Demographic models specify the historical size changes, migrations, splits and
mergers of related populations. Specifying demographic models using moments
or practically any other simulation engine can become very complicated and
error prone, especially when we want to model more than one population (e.g.
[Ragsdale2020]). Even worse, every individual software has its own language and
methods for specifying a demographic model, so a user has to reimplement the
same model across multiple software, which nobody enjoys. To resolve these
issues of reproducibility, replication, and susceptibility to errors, demes
provides a human-readable specification of complex demography that is designed
to make it easier to implement and share models and to be able to use that
demography with multiple simulation engines.
Demes models are written in YAML, and they are then automatically parsed to
create an internal representation of the demography that is readable by
moments. moments can then iterate through the epochs and demographic
events in that model and compute the SFS or LD.
Simulating the SFS and LD using a demes model
Computing expectations for the SFS or LD using a demes model is designed to
be as simple as possible. In fact, there is no need for the user to specify any
demographic events or integrate the SFS or LD objects. moments does all of
that for you.
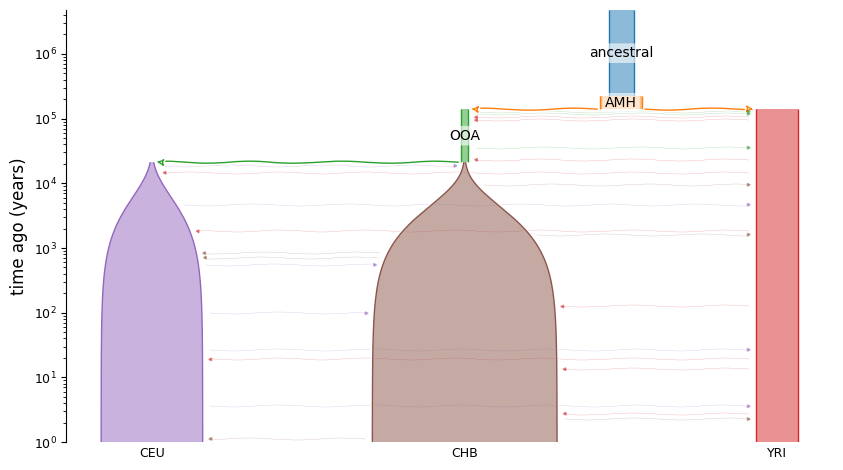
It’s easiest to see the functionality through example. In the tests directory, there is a YAML description of the [Gutenkunst2009] Out-of-African model:
description: The Gutenkunst et al. (2009) three-population model of human history.
doi:
- https://doi.org/10.1371/journal.pgen.1000695
time_units: years
generation_time: 25
demes:
- name: ancestral
description: Equilibrium/root population
epochs:
- end_time: 220e3
start_size: 7300
- name: AMH
description: Anatomically modern humans
ancestors: [ancestral]
epochs:
- end_time: 140e3
start_size: 12300
- name: OOA
description: Bottleneck out-of-Africa population
ancestors: [AMH]
epochs:
- end_time: 21.2e3
start_size: 2100
- name: YRI
description: Yoruba in Ibadan, Nigeria
ancestors: [AMH]
epochs:
- start_size: 12300
end_time: 0
- name: CEU
description: Utah Residents (CEPH) with Northern and Western European Ancestry
ancestors: [OOA]
epochs:
- start_size: 1000
end_size: 29725
end_time: 0
- name: CHB
description: Han Chinese in Beijing, China
ancestors: [OOA]
epochs:
- start_size: 510
end_size: 54090
end_time: 0
migrations:
- demes: [YRI, OOA]
rate: 25e-5
- demes: [YRI, CEU]
rate: 3e-5
- demes: [YRI, CHB]
rate: 1.9e-5
- demes: [CEU, CHB]
rate: 9.6e-5
This model describes all the populations (demes), their sizes and times of existence, their relationships to other demes (ancestors and descendents), and migration between them. To simulate using this model, we just need to specify the populations that we want to sample lineages from, the sample size in each population, and (optionally) the time of sampling. If sampling times are not given we assume we sample at present time. Ancient samples can be specified by setting sampling times greater than 0.
Let’s simulate 10 samples from each YRI, CEU, and CHB:
import moments
import numpy as np
ooa_model = "../tests/test_files/gutenkunst_ooa.yaml"
# we can visualize the model using demesdraw
import demes, demesdraw, matplotlib.pylab as plt
graph = demes.load(ooa_model)
demesdraw.tubes(graph, log_time=True, num_lines_per_migration=3);
Let’s simulate 10 samples from each YRI, CEU, and CHB:
sampled_demes = ["YRI", "CEU", "CHB"]
sample_sizes = [10, 10, 10]
fs = moments.Spectrum.from_demes(
ooa_model, sampled_demes=sampled_demes, sample_sizes=sample_sizes
)
print("populations:", fs.pop_ids)
print("sample sizes:", fs.sample_sizes)
print("FST:")
for k, v in fs.Fst(pairwise=True).items():
print(f" {k[0]}, {k[1]}: {v:.3f}")
populations: ['YRI', 'CEU', 'CHB']
sample sizes: [10 10 10]
FST:
YRI, CEU: 0.189
YRI, CHB: 0.205
CEU, CHB: 0.147
It’s that simple. We can also simulate data for a subset of the populations, while still accounting for migration with other non-sampled populations:
sampled_demes = ["YRI"]
sample_sizes = [40]
fs_yri = moments.Spectrum.from_demes(
ooa_model, sampled_demes=sampled_demes, sample_sizes=sample_sizes
)
print("populations:", fs_yri.pop_ids)
print("sample sizes:", fs_yri.sample_sizes)
print("Tajima's D =", f"{fs_yri.Tajima_D():.3}")
populations: ['YRI']
sample sizes: [40]
Tajima's D = -0.338
Ancient samples
Or sample a combination of ancient and modern samples from a population:
sampled_demes = ["CEU", "CEU"]
sample_sizes = [10, 10]
# sample size of 10 from present and 10 from 20,000 years ago
sample_times = [0, 20000]
fs_ancient = moments.Spectrum.from_demes(
ooa_model,
sampled_demes=sampled_demes,
sample_sizes=sample_sizes,
sample_times=sample_times,
)
print("populations:", fs.pop_ids)
print("sample sizes:", fs.sample_sizes)
print("FST(current, ancient) =", f"{fs.Fst():.3}")
populations: ['CEU', 'CEU_sampled_20000_0']
sample sizes: [10 10]
FST(current, ancient) = 0.0912
Note the population IDs, which are appended with “_sampled_{at_time}” where “at_time” is the generation or year (depending on the time unit of the model), as a float with an underscore replacing the decimal (here, 20000.0 years ago).
Alternative samples specification
By specifying sampled demes, sample sizes, and sample times, we have a lot
of flexibility over the sampling scheme. Samples can more simply be specified
as a dictionary, with one key per sampled population and values specifying
sample sizes. This dictionary is passed to the from_demes function using
the samples keyword, and it cannot be used in conjunction with sample times.
As such, samples are taken at the end time (most recent time) of each population.
samples = {"YRI": 10, "CEU": 20, "CHB": 30, "OOA": 10}
fs = moments.Spectrum.from_demes(ooa_model, samples=samples)
Here, samples from YRI, CEU, and CHB are taken from time zero, and the OOA sample is taken from just before its split into the CEU and CHB branches.
Linkage disequilibrium
We can similarly compute LD statistics. Here, we compute the set of multi-population Hill-Robertson statistics for the three contemporary populations (YRI, CEU, and CHB), for three different recombination rates, \(\rho=4Nr=0, 1, 2\).
import moments.LD
sampled_demes = ["YRI", "CEU", "CHB"]
y = moments.LD.LDstats.from_demes(
ooa_model, sampled_demes=sampled_demes, rho=[0, 1, 2]
)
print("sampled populations:", y.pop_ids)
sampled populations: ['YRI', 'CEU', 'CHB']
Selection and dominance in Demes.SFS
Moments can compute the SFS under selection and dominance. The demes model
format currently lets us specify a single selection and dominance coefficient
for each population in the model, or we can set different selection parameters
in each populations.
The most simple scenario is to specify a single selection and dominance
parameter that applied to all populations in the demographic model. In this
case, we can pass gamma and/or h as scalar values to the function
moments.Spectrum.from_demes():
sampled_demes = ["YRI"]
sample_sizes = [40]
gamma = 10
h = 0.1
fs_yri_sel = moments.Spectrum.from_demes(
ooa_model,
sampled_demes=sampled_demes,
sample_sizes=sample_sizes,
gamma=gamma,
h=h
)
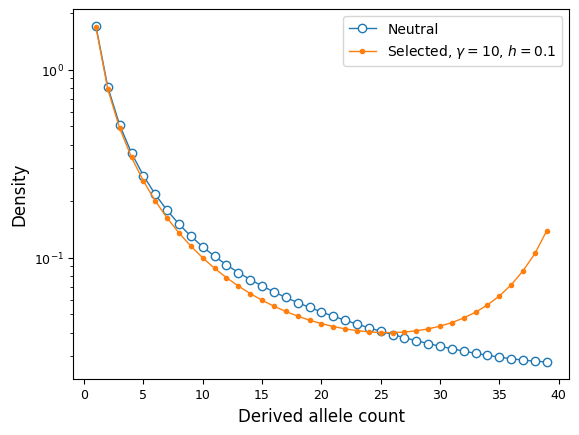
We can compare the neutral and selected spectra:
# compare to neutral SFS for YRI
fig = plt.figure()
ax = plt.subplot(111)
ax.semilogy(fs_yri, "-o", ms=6, lw=1, mfc="w", label="Neutral");
ax.semilogy(fs_yri_sel, "-o", ms=3, lw=1,
label=f"Selected, $\gamma={gamma}$, $h={h}$");
ax.set_ylabel("Density");
ax.set_xlabel("Derived allele count");
ax.legend();
We can gain more fine-grained control over variable selection and dominance in
different populations by specifying gamma and h as dictionaries mapping
population names to the coefficients. There can be as many different
coefficient values as there are different demes in the demographic model.
However, if a population is missing from the dictionary, it is assigned the
default selection or dominance coefficient. In most cases the default values
are \(\gamma = 0\) and \(h=1/2\), but these can be changed by specifying
a _default value in the selection and dominance dictionaries.
For example:
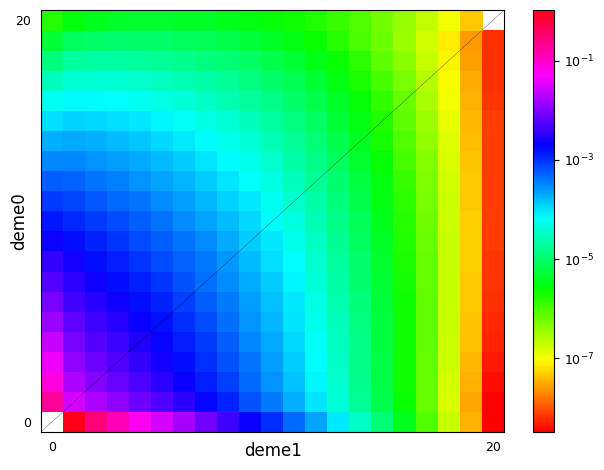
g = demes.load("data/im-parsing-example.yaml")
print(g)
gamma = {"anc": -10, "deme0": -10, "deme1": 5}
h = {"anc": 0.3, "deme0": 0.3, "deme1": 0.7}
fs = moments.Spectrum.from_demes(
g,
sampled_demes=["deme0", "deme1"],
sample_sizes=[20, 20],
gamma=gamma,
h=h
)
moments.Plotting.plot_single_2d_sfs(fs)
description: A simple isolation-with-migration model
time_units: generations
generation_time: 1
demes:
- name: anc
epochs:
- {end_time: 1500, start_size: 10000}
- name: deme0
ancestors: [anc]
epochs:
- {end_time: 0, start_size: 2000}
- name: deme1
ancestors: [anc]
epochs:
- {end_time: 0, start_size: 20000}
migrations:
- demes: [deme0, deme1]
rate: 0.0001
In the case that a demographic model has many populations but only a small subset have differing selection or dominance strengths, we can assign a default value different from \(s=0\) or \(h=1/2\). This is done by including a _default key in the dictionary (note the leading underscore, to minimize the chance that the default key conflicts with a named population in the demographic model). Taking the example above:
gamma = {"_default": -10, "deme1": 5}
h = {"_default": 0.3, "deme1": 0.7}
fs_defaults = moments.Spectrum.from_demes(
g,
sampled_demes=["deme0", "deme1"],
sample_sizes=[20, 20],
gamma=gamma,
h=h
)
assert np.allclose(fs, fs_defaults)
Using Demes to infer demography
Above, we showed how to use moments and demes-based demographic models
to compute expectations for static demographic models. That is, given a fixed
demography we can compute expectations for the SFS or LD. We often want to
optimize the parameters of a given demographic model to fit observations from
data. The general idea is that we specify a parameterized model, compute the
expected SFS under that model and its likelihood given the data, and then
update the model parameters to improve the fit. Moments uses scipy’s
optimization functions to perform
optimization.
To run the inference, we need three items: 1) the data (SFS) to be fit, 2)
a parameterized demographic model, and 3) a way to tell the optimization
function which parameters to fit and any constraints on those parameters. We’ll
assume you already have a data SFS with stored pop_ids. For example, the
data could be a 3-dimensional SFS for the three sampled populations in the
Out-of-Africa demographic model above, so that data.pop_ids = ["YRI", "CEU",
"CHB"].
The second item is the demes-formatted demographic model, such as the model
written above. In this model, the parameter values are the demographic event
times, population sizes, and migration rates, and the YAML file specifies all
fixed parameters and initial guesses for the parameters to be fit.
The third item is a separate YAML-formatted file that tells the optimization function the variable parameters that should be fit and any bounds and/or inequality constraints on the parameter values.
The options file
All parameters to be fit must be included under parameters in the option
file. Any parameter that is not included here is assumed to be a fixed
parameter, and it will remain the value given in the Demes graph. moments
will read this YAML file into a dictionary using a YAML parser, so it needs to
be valid and properly formatted YAML code.
The only required field in the “options” YAML is parameters. For each
parameter to be fit, we must name that parameter, which can be any unique
string, and we need to specify which values in the Demes graph correspond to
that value (optionally, we can include a parameter description for our own
sake). For example, to fit the bottleneck size in the Out-of-Africa model, our
options file would look like:
parameters:
- name: N_B
description: Bottleneck size for Eurasian populations
values:
- demes:
OOA:
epochs:
0: start_size
lower_bound: 100
upper_bound: 100000
This specifies that the start size of the first (and only) epoch of the OOA deme in the Demes graph should be fit. We have also specified that the fit for this parameter should be bounded between 100 and 100,000.
The same parameter can affect multiple values in the Demes graph. For example,
the size of the African population in the Out-of-Africa model is applied to
both the AMH and the YRI demes. This simply requires adding additional keys in
the values entry:
parameters:
- name: N_A
description: Expansion size
values:
- demes:
AMH:
epochs:
0: start_size
YRI:
epochs:
0: start_size
lower_bound: 100
upper_bound: 100000
Migration rates can be specified to be fit as well. Note that the index of the migration is given, pointing to the migrations in the order they are specified in the demes file.
parameters:
- name: m_Af_Eu
description: Symmetric migration rate between Afr and Eur populations
upper_bound: 1e-3
values:
- migrations:
1: rate
Note here that we have specified the upper bound to be 1e-3 (the units of
the migration rate are parental migrant probabilities, typical in population
genetics models). For any parameter, we can set the lower bound and upper bound
as shown here. If they are not given, the lower bound defaults to 0 and the
upper bound defaults to infinity.
Finally, we can also specify constraints on parameters. For example, if some event necessarily occurs before another, we should add that relationship to the list of constraints.
parameters:
- name: TA
description: Time before present of ancestral expansion
values:
- demes:
ancestral:
epochs:
0: end_time
- name: TB
description: Time of YRI-OOA split
values:
- demes:
AMH:
epochs:
0: end_time
- name: TF
description: Time of CEU-CHB split
values:
- demes:
OOA:
epochs:
0: end_time
constraints:
- params: [TA, TB]
constraint: greater_than
- params: [TB, TF]
constraint: greater_than
This specifies each of the event timings in the OOA model to be fit, and the
constraints say that TA must be greater than TB, and TB must be
greater than TF.
The inference function
To run optimization using the Demes modeul, we call
moments.Demes.Inference.optimize. The first three required inputs to
optimize are the Demes input graph, the parameter options, and the data, in
that order.
Additional options can be passed to the optimization function using keyword
arguments in the moments.Demes.Inference.optimize function. These include:
maxiter: Maximum number of iterations to run optimization. Defaults to 1,000.perturb: Defaults to 0 (no perturbation of initial parameters). If greater than zero, it perturbs the initial parameters by up toperturb-fold. So ifperturbis 1, initial parameters are randomly chosen from \([1/2\times p_0, 2\times p_0]\). Larger values result in stronger perturbation of initial guesses.verbose: Defaults to 0. If greater than zero, it prints an update to the specifiedoutput_stream(which defaults tosys.stdout) everyverboseiterations.uL: Defaults to None. If given, this is the product of the per-base mutation rate and the length of the callable genome used to compile the data SFS. If we don’t give this scaled mutation rate, we optimize with theta as a free parameter. Otherwise, we optimize with theta given by \(\theta=4 \times N_e \times uL\), and \(N_e\) is taken to be the size of the root/ancestral deme (for which the size can be a either be a fixed parameter or a parameter to be fit!).log: Defaults to True. If True, optimize the log of the parameters.method: The optimization method to use, currently with the options “fmin” (Nelder-Mead), “powell”, or “lbfgsb”. Defaults to “fmin”.fit_ancestral_misid: Defaults to False, and cannot be used with a folded SFS. For an unfolded SFS, the ancestral state may be misidentified, resulting in a distortion of the SFS. We can account for that distortion by fitting a parameter that accounts for some fraction of mis-labeled ancestral states.misid_guess: Used withfit_ancestral_misid, as the initial ancestral misidentification parameter guess. Defaults to 0.02.output_stream: Defaults to sys.stdout.output: Defaults to None, in which case the result is printed to theoutput_stream. If given, write the optimized Demes graph in YAML format to the given path/filename.overwrite: Defaults to False. If True, we overwrite any file with the path/filename given byoutput.
Single-population inference example
To demonstrate, we’ll fit a simple single-population demographic model to the synonymous variant SFS in the Mende (MSL) from the Thousand Genomes data. The data for this population is stored in the docs/data directory. We previous parsed all coding variation and used a mutation model to estimate \(u\times L\).
We can either fold the frequency spectrum, which is useful when we do not know the ancestral states of mutations. Alternatively, we can fit with the unfolded spectrum, and if we suspect that some proportion of SNPs have their ancestral state misidentified, we can additionally fit a parameter that corrects for this uncertainty. We’ll take the second approach here, and fit the unfolded spectrum.
import moments
import pickle
all_data = pickle.load(open("./data/msl_data.bp", "rb"))
data = all_data["spectra"]["syn"]
data.pop_ids = ["MSL"]
uL = all_data["rates"]["syn"]
print("scaled mutation rate (u_syn * L):", uL)
# project down to a smaller sample size, for illustration purposes
data = data.project([30])
scaled mutation rate (u_syn * L): 0.14419746897690008
We’ll fit a demographic model that includes an ancient expansion and a more recent exponential growth. This initial model is stored in the docs/data directory as well.
The YAML specification of this model is
description: A single-population model to be fit to the MSL data. Initial guesses
are given as parameters in the model.
time_units: years
generation_time: 29
demes:
- name: MSL
epochs:
- end_time: 350000
start_size: 10000
- end_time: 20000
start_size: 25000
- end_time: 0
end_size: 60000
And we can specify that we want to fit the times of the size changes, and all population sizes. (Note that if we did not have an estimate for the mutation rate, we would not fit the ancestral size.)
parameters:
- name: T1
description: Time before present of ancestral expansion
values:
- demes:
MSL:
epochs:
0: end_time
- name: T2
description: Time before present of start of exponential growth.
values:
- demes:
MSL:
epochs:
1: end_time
- name: Ne
description: Effective (ancestral/root) size
values:
- demes:
MSL:
epochs:
0: start_size
- name: NA
description: Ancestral expansion size
values:
- demes:
MSL:
epochs:
1: start_size
- name: NF
description: Final population size
values:
- demes:
MSL:
epochs:
2: end_size
constraints:
- params: [T1, T2]
constraint: greater_than
deme_graph = "./data/msl_initial_model.yaml"
options = "./data/msl_options.yaml"
And now we can run the inference:
output = "./data/msl_best_fit_model.yaml"
ret = moments.Demes.Inference.optimize(
deme_graph,
options,
data,
uL=uL,
fit_ancestral_misid=True,
misid_guess=0.01,
method="lbfgsb",
output=output,
overwrite=True
)
param_names, opt_params, LL = ret
print("Log-likelihood:", -LL)
print("Best fit parameters")
for n, p in zip(param_names, opt_params):
print(f"{n}\t{p:.3}")
Log-likelihood: -126.08823318048917
Best fit parameters
T1 4.38e+05
T2 2.2e+04
Ne 1.09e+04
NA 2.5e+04
NF 6.6e+04
p_misid 0.026
Printed above are the best fit parameters for this model, including the
ancestral misidentification rate for synonymous variants in the Mende sample.
Parameters in this fit are scaled by our estimate of the total mutation rate of
synonymous variants (uL), which allows us to infer the ancestral
\(N_e\). Below, we plot the results and then compute confidence intervals
for this fit.
Plotting the results
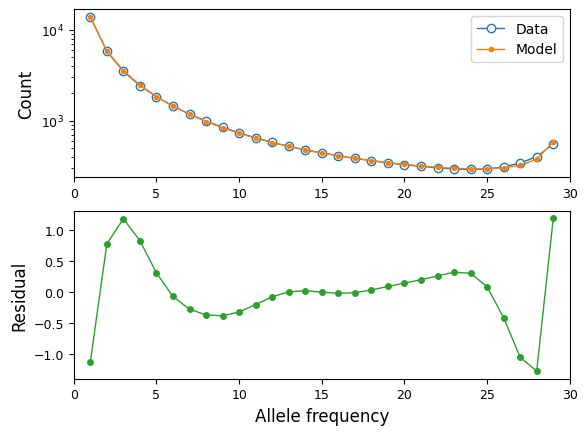
We can see how well our best fit model fits the data, using moments
plotting features:
fs = moments.Spectrum.from_demes(output, samples={"MSL": data.sample_sizes})
fs = moments.Misc.flip_ancestral_misid(fs, opt_params[-1])
moments.Plotting.plot_1d_comp_multinom(fs, data)
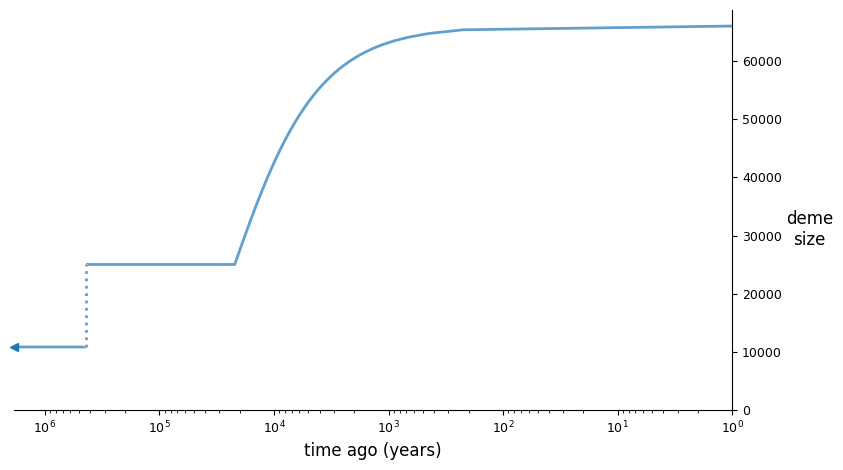
And we can illustrate the best fit model using demesdraw:
import demes, demesdraw
opt_model = demes.load(output)
demesdraw.size_history(opt_model, invert_x=True, log_time=True);
Computing confidence intervals
Using the output YAML from moments.Demes.Inference.optimize(), we compute
confidence intervals using moments.Demes.Inference.uncerts(). This function
takes the output Demes graph from the optimization, the same parameter options
file, and the same data used in inference. These need to be consistent between
the optimization and uncertainty computation. If we specified the mutation rate
or inferred an ancestral misidentification parameter, those must also be provided.
The additional options to uncerts() are
bootstraps: Defaults to None, in which case we use the FIM approach.uL: The scaled mutation rate, if used in the optimization. (See above for details.)log: Defaults to False. If True, we assume a log-normal distribution of parameters. Returned values are then the standard deviations of the logs of the parameter values, which can be interpreted as relative parameter uncertainties.eps: The relative step size to use when numerically computing derivatives to estimate the curvature of the likelihood function at the inferred best-fit parameters.method: Defaults to “FIM”, which uses the Fisher information matrix. We can also use the Godambe information matrix, which uses bootstrap replicates to account for non-independence between linked SNPs. This uses methods developed by Alec Coffman in Ryan Gutenkunst’s group, described in [Coffman2016].fit_ancestral_misid: If the ancestral misid was fit, this should be set to True.misid_fit: The fit misidentification parameter, if it was fit.output_stream: Defaults to sys.stdout.
In our example using the Mende data above, we’ll use the FIM method compute
confidence intervals:
std_err = moments.Demes.Inference.uncerts(
output,
options,
data,
uL=uL,
fit_ancestral_misid=True,
misid_fit=opt_params[-1],
)
print("95% CIs")
print("param\t\t2.5%\t\t97.5%")
for n, p, e in zip(param_names, opt_params, std_err):
print(f"{n}\t{p - 1.96 * e:-12g}\t{p + 1.96 * e:-13g}")
95% CIs
param 2.5% 97.5%
T1 378253 497820
T2 10528.9 33528.2
Ne 10387.3 11316.9
NA 23521.2 26539.5
NF 41670.7 90313.3
p_misid 0.0228469 0.0291068
To compute standard errors that account for non-independence between SNPs, we
would use method="GIM" and include a list of bootstrap replicate spectra
that we pass to bootstraps.
Two-population inference and uncertainty example
Here, we’ll simulate a demographic model using msprime. In this example,
we’ll simulate many regions of varying length and mutation rates, from which we
compute uL and estimate confidences using the GIM method, which
requires bootstrapped datasets of the SFS and associated scaled mutation rates.
First, we’ll simulate data under this two-population model:
g = demes.load("./data/two-deme-example.yaml")
print(g)
time_units: generations
generation_time: 1
demes:
- name: anc
epochs:
- {end_time: 2000, start_size: 8500}
- name: A
ancestors: [anc]
epochs:
- {end_time: 0, start_size: 700, end_size: 11000}
- name: B
ancestors: [anc]
epochs:
- {end_time: 0, start_size: 17500}
migrations:
- demes: [A, B]
rate: 0.0015
import msprime
demog = msprime.Demography.from_demes(g)
num_regions = 200
# Lengths between 75 and 125 kb
Ls = np.random.randint(75000, 125000, 200)
# Mutation rates between 1e-8 and 2e-8
us = 1e-8 + 1e-8 * np.random.rand(200)
# Total mutation rate
uL = np.sum(us * Ls)
# Simulate and store allele frequency data (summed and by region)
ns = [20, 20]
region_data = {}
data = moments.Spectrum(np.zeros((ns[0] + 1, ns[1] + 1)))
data.pop_ids = ["A", "B"]
# sample_sets are required to get the SFS from the tree sequences
sample_sets = (range(20), range(20, 40))
for i, (u, L) in enumerate(zip(us, Ls)):
ts = msprime.sim_ancestry(
{"A": ns[0] // 2, "B": ns[1] // 2},
demography=demog,
recombination_rate=1e-8,
sequence_length=L,
)
ts = msprime.sim_mutations(ts, rate=u)
SFS = ts.allele_frequency_spectrum(
sample_sets=sample_sets, span_normalise=False, polarised=True)
region_data[i] = {"uL": u * L, "SFS": SFS}
data += SFS
print("Simulated data. FST =", data.Fst())
Simulated data. FST = 0.03488586466502664
With this simulated data, we can now re-infer the model, using the following options:
parameters:
- name: T
description: Ancestral split time
values:
- demes:
anc:
epochs:
0: end_time
- name: Ne
description: Ancestral effective population size
values:
- demes:
anc:
epochs:
0: start_size
- name: NA0
description: Initial population size of A
values:
- demes:
A:
epochs:
0: start_size
- name: NA
description: Final population size of A
values:
- demes:
A:
epochs:
0: end_size
- name: NB
description: B population size
values:
- demes:
B:
epochs:
0: start_size
- name: M
description: migration rate between A and B
values:
- migrations:
0: rate
upper_bound: 1
deme_graph = "./data/two-deme-example.yaml"
options = "./data/two-deme-example-options.yaml"
output = "./data/two-deme-example-best-fit.yaml"
ret = moments.Demes.Inference.optimize(
deme_graph,
options,
data,
uL=uL,
perturb=1,
output=output,
overwrite=True
)
Printing the results of this inference run:
param_names, opt_params, LL = ret
print("Log-likelihood:", -LL)
print("Best fit parameters")
for n, p in zip(param_names, opt_params):
print(f"{n}\t{p:.3}")
Log-likelihood: -1296.725088604149
Best fit parameters
T 1.52e+03
Ne 8.61e+03
NA0 5.74e+02
NA 2.05e+04
NB 1.46e+04
M 0.00115
To compute confidence intervals using the Godambe method, we need generate bootstrap replicates of the data (and scaled mutation rate, if specified in the optimization).
bootstraps = []
bootstraps_uL = []
for _ in range(len(region_data)):
choices = np.random.choice(range(200), 200, replace=True)
bootstraps.append(
moments.Spectrum(sum([region_data[c]["SFS"] for c in choices])))
bootstraps_uL.append(sum([region_data[c]["uL"] for c in choices]))
Computing the uncertainties using GIM requires passing the bootstrapped
data:
std_err = moments.Demes.Inference.uncerts(
output,
options,
data,
bootstraps=bootstraps,
uL=uL,
bootstraps_uL=bootstraps_uL,
method="GIM",
)
print("Standard errors:")
print("param\t\topt\t\tstderr")
for n, p, e in zip(param_names, opt_params, std_err):
print(f"{n}\t{p:-11g}\t{e:-14g}")
Standard errors:
param opt stderr
T 1515.2 183.786
Ne 8607.87 179.118
NA0 573.705 84.0684
NA 20466 5675.2
NB 14610.3 1994.22
M 0.00115135 0.000150782
References
Gutenkunst, Ryan N., et al. “Inferring the joint demographic history of multiple populations from multidimensional SNP frequency data.” PLoS genet 5.10 (2009): e1000695.
Ragsdale, Aaron P., et al. “Lessons learned from bugs in models of human history.” The American Journal of Human Genetics 107.4 (2020): 583-588.